Formal Reasoning About Layered Monadic Interpreters

Our paper extends the Coq Interaction Trees library to support elegant reasoning about layered monadic interpreters. This artifact contains the corresponding formalism, and the case study of an Imp2Asm compiler.

Documentation

This documentation includes pretty-printed Coq source, which can also be found as .v files in the git repository. The pretty-printed html hides proof scripts by default, so you can click on Show Proofs at the top of the page to display all proofs.

Proof Structure

This artifact builds on top of the Interaction Tree library, and this artifact includes the original ITree library along with the relevant extension which is the contribution of the paper. The Coq contribution of this artifact is outlined in these following files. N.B. There are other files included in the table of contents and the artifact submission which are part of the original ITree library.

Core

Subevent.v: Defines extensible subevents with automatic injection.

Interp

HFunctor.v: Defines higher-order functors and laws.
Interp.v: Defines interpretations of iterative monads.
InterpFacts.v: Defines interpretation laws.

EqmR

EqmRMonad.v: Defines eqmR well-formedness laws, eqmR monad laws and inversion laws.
EqmRMonadH.v: Defines eqmR relations over different monads.
EqmRMonadT.v: Defines lifting of eqmR relations over monad transformers.
ITree_strong.v: Proves eqmR-related laws for interaction trees with strong bisimulation.
ITree_weak.v: Proves eqmR-related laws for interaction trees with weak bisimulation.
State.v: Proves eqmR-related laws for state monad.
Prop.v: Proves eqmR-related laws for prop monad.
StateT.v: Proves eqmR-related laws for state monad transformer.
Error.v: Proves eqmR-related laws for error monad.
ErrorT.v: Proves eqmR-related laws for error monad transformer.
ID.v: Proves eqmR-related laws for identity monad.

Basics

HeterogeneousRelations.v: Helper and utility lemmas for heterogeneous relations.
MonadState.v: Proves iterative laws for state monad.
MonadFail.v: Proves iterative laws for error monad.

Paper Correspondence

Below is a table that shows how the definition of laws and their instances correspond to the Coq mechanization. /

Paper			Coq Proof
Item	Description	Subitems	File	Name
Section 3.1, 3.2	Building Layered Monadic Interpreters	Trigger	Subevent.v	Class Trigger
		Subevent		Class Subevent
		Subevent Instances		Section Subevent_Instances
Section 3.4	Interpretable monads	Interp	Interp.v	Class Interp
		HFunctor	HFunctor.v	Class HFunctor
		stack_interp	InterpFacts.v	Instance stack_interp
Figure 7	Well-formedness Laws of EqmR		EqmRMonad.v	Class EqmR_OK
Section 4.2	Image of a Monadic Computation		EqmRMonad.v	Definition mayRet
Figure 8	EqmRMonad Laws		EqmRMonad.v	Class EqmRMonadLaws
Figure 9	EqmRMonadInverses Laws		EqmRMonad.v	Class EqmRMonadInversionProperties
Section 4.1-4.3	ID Monad Instance for EqmR		ID.v
Section 4.1-4.3	State Monad Instance for EqmR Laws		State.v
Section 4.1-4.3	State Monad Instance for EqmR Laws		State.v
Section 4.1-4.3	Error Monad Instance for EqmR Laws		Error.v
Section 4.1-4.3	ITree Monad Instance for EqmR Laws (strong bisimulation)	Leaves	ITree_strong.v	Returns
Section 4.1-4.3	ITree Monad Instance for EqmR Laws (weak bisimulation)	Leaves	ITree_weak.v	Returns
Section 4.1-4.3	Prop Monad Instance for EqmR Laws		Prop.v
Figure 10	Monad morphism laws		EqmRMonadT.v	Section MonadMorphism
Figure 11*	Monad transformer well-formedness conditions		EqmRMonadT.v	Class MonadTLaws
Section 4.4	StateT Monad Transformer Law Instance		StateT.v
Section 4.4	ErrorT Monad Transformer Law Instance		ErrorT.v
Section 4.5	Relating Computation across Distinct Monads		EqmRMonadH.v
Figure 12	Interpretation laws		InterpFacts.v
Figure 13	Higher-order functor laws		HFunctor.v
Figure 14	Composable Structures and Laws	MonadT Laws	EqmRMonadT.v	compose_MonadT
		IterativeMonadT		compose_IterativeMonadT
		IterativeMonadT Laws		compose_WF_IterativeMonadT
		HFunctor	HFunctor.v	compose_HFunctor
		HFunctor Laws	HFunctor.v	compose_WF_HFunctor

* N.B. : The MonadMorphism laws is parameterized over a monad morphism from monad M to monad MT, while the MonadTLaws is parameterized over a monad transformer. Figure 11 is not explicitly stated as a typeclass but is proved for the state and error transformers (in stateT and errorT).

Case Study

The case study in Section 6 is in tutorial/, where the definition of languages are in Imp.v and Asm.v, and the proof of correctness for the compiler is in Imp2AsmCorrectness.v. The commuted version of this proof mentioned in Section 6.2.3 is in tutorial_commute/. The custom tactics mentioned is in tutorial/Proofmode.v.

Typeclass dependencies

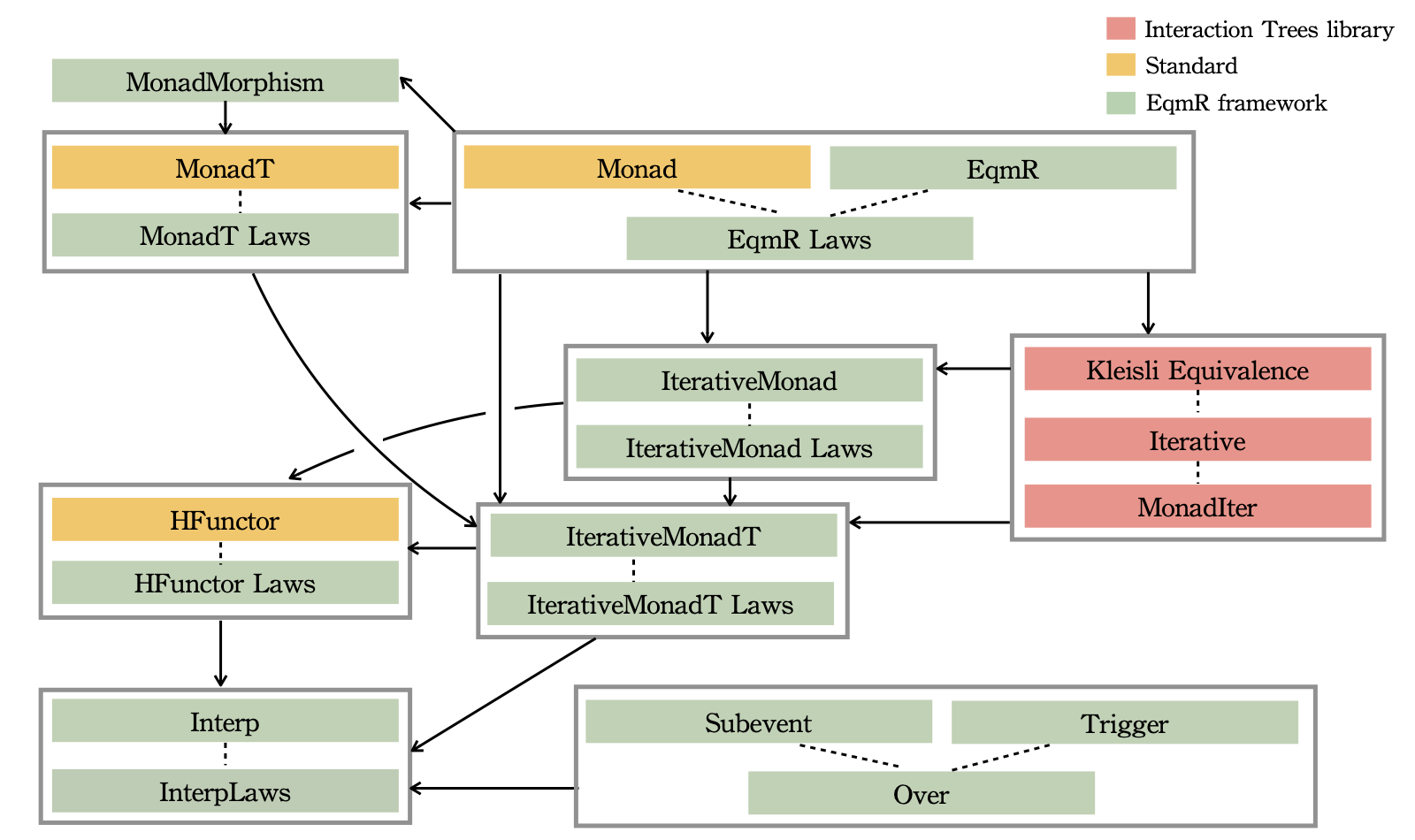
Typeclass dependency in EqmR Framework is shown above. The red nodes are the category theory-relevant typeclasses from the Interaction Trees library (most notably the theory of iterative monads and equivalence on Kleisli arrows), the yellow nodes are standard functional programming typeclasses (functor, monad, monad transformers, higher-order functors), and the green nodes represent the structural properties that we have formalized in the framework. A dotted line connects an "operational" typeclass to its corresponding laws, and solid arrows represent dependencies.